A complete preprint of the book
- Josef Dick and Friedrich Pillichshammer, Digital Nets and Sequences. Discrepancy Theory and Quasi-Monte Carlo Integration. Cambridge University Press, Cambridge, 2010. © Cambridge University Press.
is now available here. The final published version can be obtained directly from Cambridge University Press here.
The preprint version differs of course from the final version, for instance, the page numbers are different. However, the numbering of Chapters, Sections, Theorems, Lemmas, Corollaries, Definitions and Examples is the same in both versions. The list of corrections is for the published version. We do not have a separate list for the preprint version (though the corrections for the published version also apply to the preprint version).
-nets and Sudoku and then generalize the Sudoku in analogy to higher order 
-nets in base 3. A new type of Sudoku puzzle is presented at the end. 
and for higher order sequences we have the parameters 
and sequences 
such that ![\displaystyle \left|\int_{[0,1]^s} f(\boldsymbol{x}) \,\mathrm{d} \boldsymbol{x} - \frac{1}{N} \sum_{n=0}^{N-1} f(\boldsymbol{x}_n) \right| = \mathcal{O} (N^{-\alpha} (\log N)^{\alpha s}),](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cleft%7C%5Cint_%7B%5B0%2C1%5D%5Es%7D+f%28%5Cboldsymbol%7Bx%7D%29+%5C%2C%5Cmathrm%7Bd%7D+%5Cboldsymbol%7Bx%7D+-+%5Cfrac%7B1%7D%7BN%7D+%5Csum_%7Bn%3D0%7D%5E%7BN-1%7D+f%28%5Cboldsymbol%7Bx%7D_n%29+%5Cright%7C+%3D+%5Cmathcal%7BO%7D+%28N%5E%7B-%5Calpha%7D+%28%5Clog+N%29%5E%7B%5Calpha+s%7D%29%2C+&bg=ffffff&fg=333333&s=0&c=20201002)
is the number of quadrature points and 
is the smoothness of the integrand 
factor) and this can also be observed from some simple numerical examples shown in the paper (note that the figures in the paper show the standard deviation (or root mean square error) and not the variance of the estimator). In this post you can also find Matlab programs which generate the quadrature points introduced in this paper and a program to generate the numerical results shown in the paper. 
where 
for digital nets and 
for digital sequences (for more background information on this topic see ![\displaystyle \left|\int_{[0,1]^s} f(\boldsymbol{x}) \, \mathrm{d} \boldsymbol{x} - \frac{1}{b^m} \sum_{n=0}^{b^m-1} f(\boldsymbol{x}_n) \right| \le C_{s,\alpha} \frac{(\log N)^{s \alpha}}{N^\alpha}, \hspace{2cm} (1)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cleft%7C%5Cint_%7B%5B0%2C1%5D%5Es%7D+f%28%5Cboldsymbol%7Bx%7D%29+%5C%2C+%5Cmathrm%7Bd%7D+%5Cboldsymbol%7Bx%7D++-++%5Cfrac%7B1%7D%7Bb%5Em%7D+%5Csum_%7Bn%3D0%7D%5E%7Bb%5Em-1%7D+f%28%5Cboldsymbol%7Bx%7D_n%29+%5Cright%7C++%5Cle+C_%7Bs%2C%5Calpha%7D+%5Cfrac%7B%28%5Clog+N%29%5E%7Bs+%5Calpha%7D%7D%7BN%5E%5Calpha%7D%2C+%5Chspace%7B2cm%7D+%281%29+&bg=ffffff&fg=333333&s=0&c=20201002)
is the smoothness of the integrand 
and 
is a constant which only depends on 
and 
(but not on 
For instance, if 
in each variable, then we get a convergence rate of 
where 
is the number of quadrature points used in the approximation and 
can be chosen arbitrarily small. If 
derivatives then we get a convergence of 
and so on.
. This allows us to find good higher order polynomial lattice rules for weighted function spaces. It also presents a feasible alternative to the direct construction introduced in 
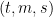-nets have a higher order analogue. This applies to digital as well as geometric nets. Additionally there are also some further propagation rules which do not exist for classical nets (for example the higher order to higher order construction). The higher order to higher order propagation rule is, as of now, still the only method to obtain higher order nets from classical nets. Fortunately it works in the digital as well as geometric case.
Quasi-Random Ideas. 